Parallel Partitioning via SRF

2010-11-11

James R. Holten III, PhD
Institute for Complex Additive Systems Analysis (ICASA)
New Mexico Institute of Mining and Technology (NMT)
Socorro, NM, 87801

Abstract

This paper describes how the concepts of the SRF Algebra may be applied to define the steps needed in partitioning a large data model and to generate the communications maps needed to effectively pass the necessary data between process partitions. Using the partitioning and communications map descriptive metadata the paper also shows how the various load types: processing loads, partition sizes, and communications loading, may be included in the partition assignments decisions. The algorithms defined via the SRF metadata is then easily converted directly into code to perform that partitioning and other defined operations on any application represented using the SRF data model. The partitioning is generalized, and allows any number of partitions. The approach itself is being parallelized for use on exascale HPC applications.

I. Overview

The SRF (Sets, Relations, and Fields) Algebra [1,2] was devised as an metadata abstraction for basic data_model representation and manipulation. The abstraction provides a standard for a simple description of data object collections. The descriptions, in turn, enable expressing the data object interrelationships, data structure algorithm operations on those data objects, and data structure related analysis steps. The basic representation of data relationship allows concepts and data objects from one application domain to be easily shared by developers and analysts in other application domains. The abstractions also allow merging the data structures and data relationships of multiple diverse models into a single application code. Models and programs developed using the abstractions of the SRF Algebra have been built, and those implementations demonstrate how data and analysis tools can be easily constructed to be shared among diverse application codes.

SRF models have been generated for generalized mesh models, finite element mesh models, molecular models, particle models, and generalized network models. The concepts and algorithms presented in this paper may be applied to SRF models of any of these forms.

This paper presents how to apply basic parallel partitioning concepts to SRF-based model descriptions for easy conversion to data-parallel constructs for an arbitrary number of processor partitions, and can include model element and partition weighting calculations for estimating partition data sizes, processing loads, and communications loads for load balancing across the process partitions and communications channels.

A. Background

To enable sequential programs to be scaled up to handle extremely large problems the programs must have their data partitioned and parts of the data assigned to each of the allotted processors for parallel execution of their algorithms [6,12]. The complexities of partitioning data for extremely large and complex problems so they can be ported onto parallel architectures cause many model developers to fall back on the old standby approach of using structured (usually rectangular mesh) models and dividing the problem by an integral number of segments in each dimension, generally via recursive coordinate bisection (RCB). These choices force the partitioning to be dependent on adjacent rectangular blocks of a predefined size and number, and cannot be easily adjusted in size to allow for balancing the computational and communications loads across the processors or communications links. Often this restricts the programmer to assume homogeneous processor and communications characteristics, preventing the use of the partitioned problem on distributed and nonhomogeneous parallel architectures.

Historical efforts have shown that fixed-sized meshes are impractical for many applications, as adaptive mesh refinements (AMR) allow generating finer resolution around "interesting" regions in the model, so overlays of regions of finer rectangular meshes are commonly used [8,12]. Also the rectangularly structured mesh model approach is useless for large-scaled network models such as those needed in modeling critical infrastructure networks using graphs and network flow models. Similarly a more general representation is usually needed for molecular and particle models.

The SRF Algebra [1] is based on abstract sets of objects, fields of properties or attributes for each of those objects, and relations describing the associations between pairs of members of a single set of objects, or between members of a pair of distinct object sets. The abstraction maps easily to collections of objects as class instances, as in C++ and Java codes, arrays of structs as in C code, or the multiple arrays of properties common in older FORTRAN codes.

Sets, Relations, and Fields Example Picture

Figure 1: Sets, Relations, and Fields Example

The basic SRF objects that must exist in most complex data models are as follows:

The data model object sets, though only three element sets are used here, but the concepts can be extended for any number of element type sets:
- S_me -- The set of major elements for the model. These may be assemblies in a machine model, spatial zones in a mesh model, nodes in a critical infrastructure network model, people or objects in a social network model.
- S_se -- The set of secondary elements for the model. These can be parts in a mechanical model, zone region faces for a mesh model, or links in a network model.
- S_te -- The set of tertiary elements for the model. These may be mesh zones over parts in a mechanical model, vertices in a mesh model, or subnets in a network model.
- Many other levels of dependent element sets may be included in any given model, forming dependency chains or trees from the major elements chosen for the model.
The data model object set relations:
- R_se,me -- The mapping of secondary elements to the major elements that depend on them.
- R_te,se -- The mapping of tertiary elements to the secondary elements that depend on them.
The data model object property fields. There can be any number of them over each of the elements sets listed above. They will be referenced as:
- F_f[j],me -- The jth field of values over the major element set.
- F_f[j],se -- The jth field of values over the secondary element set.
- F_f[j],te -- The jth field of values over the tertiary element set.

The element set dependencies are of two forms, directly dependent on the major element set, as in S_se via R_se,me, or indirectly dependent, as in S_te via R_te,se and R_se,me. To extend this pattern to any number of additional element sets their various interdependencies must be identified and be traceable back to the major elements upon which the data partitioning is based. Also, for extremely complex models the dependencies may form a dependency tree, but all the dependencies must still eventually be traceable back to a major element set. By using the SRF Algebra notation the roadmap that is developed can be used for partitioning any data model in the described forms.

Figure 2: Element Set Dependencies Forms

In the various commonly used model representations much of the information about the object associations is often implicit. It is only present in the code variable references, the indexing into associated arrays of dependent object properties, and the colocation of data fields and methods in struct or class objects. To understand the relationships between various modeled object types one must reverse engineer the intent of the implementer. The data associations intended by the programmer or model developer is often not obvious to the reader from the data organization or from the code unless it is described in comments or supporting documents. Because of this obscurity of intent mistakes are easily made when updating or parallelizing the code, either from simple oversights, not realizing the significance of awkward code, or from gross misunderstanding of intent when scaling the code in these models for larger problem sizes. This can happen regardless of the programming languages used because of the obscurity that implicit relationships provide.

Much of the complexity of of partitioning data onto parallel processors comes from determining which data must be shared between processors. Here a few terms must be defined for the purposes of this paper:

full: All the data objects which must be present in the partitions or in the overall program data model, including all the private and share objects when referenced relative to any given partition.
own: those data object whose field values are computed on that partition's processor, including private and pass categories below, are considered "owned" by that partition.
share: those data objects whose field values are computed on this or another partition's processor and must be copied (shared) between processors, including both pass and receive categories of data model elements below.

Figure 3: Full vs Own vs Share Example
private: those data object whose field values are of category own for a given partition and are not in the category share for any partition.
pass: those data objects whose field values are computed locally (category own) and must be copied to one or more other partition's processors. They are in both categories own and share.
receive: those data objects whose field values are computed on some other partition's processor and must be copied (shared) to the given processor partition. They are those members that are in the share category, but not in the own or pass categories.

Figure 4: Private vs Pass vs Receive Example
ghost region: a subset of major element "neighbors" which the partition does not own, but whose values must be available in the partition to perform calculations on all the major elements that the partition does own. Some algorithms require the presence of multiple layers of ghost regions, including neighbors one, two, or more links distant outside the partition's own subset of major elements.

Figure 5: Levels of Ghost Regions
shadow region: the secondary and tertiary elements whose values must be available in multiple partitions to perform calculations on the own major and other elements in the partitions. These are the share secondary and tertiary elements for each partition.

Figure 6: Shadow Regions -- Shared Dependent Elements

Putting code data models into the conventions of SRF representations makes the relevant data relationships explicit. This paper describes how to utilize these explicit relationships to enable the partitioning needed to scale up the problem sizes, even to exascale extremes.

B. The Approach

The metadata abstractions provided by the SRF Algebra data model provide the mechanism for describing the relationship of data partitioning constructs to the parts of the modeled data. In this paper the description of the partitioning is derived, then it is used to describe the creation of communications maps. Once the partitioning and communications relationships are derived and presented methods for calculating loading estimates and comparing limitations relative to assigning partitions to system resources (processors and communications links) are discussed.

In this document, when an expression is derived that can be generically applied to any of the element types above, the generic E will be used instead of repeating the derivation for each of me, se, or te element sets.

There are generally two types of data passing steps for which data sharing patterns must be considered. One is at each time step, and the other is on each iteration step for some iterative operations within a time step. Also, the complexity of generating sharing maps can be amplified by having different elements use different time step sizes. This paper focuses its efforts on the basics by assuming only fixed time step sharing is needed, however the derived procedures may easily be applied to the other sharing type and nonhomogeneous time step sizes as well.

The "Partitioning Elements" section describes how the partitioning of the major elements is projected via composition of relations to the other model element types, and how those projections identify which elements must have their field values shared across partition boundaries. It also defines which partitions in a partitioning of the model must communicate (share data) with which other partitions.

The "Communications Maps" section shows how ownership of an element indicates which partition does the calculation of values for that element, preventing one category of potential race conditions. This also resolves which are the partitions with whom the calculated values must be shared. It then shows how the ownership and sharing can be converted to identify, in detail, which elements' field values must be communicated to each of the partition's "neighbors".

The "Calculating Loads" section describes various methods for describing loading through calculating partition data sizes, partition computation requirements, and communications link transfer volume needs. It then discusses how any given configuration of element ownership by the partitions, through the use of the partition relations and the communications maps, can estimate those expected loads for each partition and communications path. Once these load types are discussed methods of "load shifting" to create a more load-balanced assignment of elements to partitions are also discussed.

The final section discusses a collection of applicable concepts and techniques, including

How to convert rectangularly structured data models, common in the computational fluid dynamics (CFD) simulation world, into the generalized SRF data model form so the concepts may be easily applied and
The application of SRF concepts to handling exascale problem sizes.

II. Partitioning Elements

In order to allocate parts of a large data model onto multiple processors and coordinate the activities on these processors the developer must be able to partition the data for data-parallel processing. The developer can then use that partitioning and the data element type interdependencies to determine what to communicate between each pair of processors.

The first step in dividing the data elements among the processors is to create a set of partitions, with one partition for each processor. Then by assuming that an assignment of the major elements to each processor partition can be made, the needed data model manipulations can be defined. The partitioned major element to partition assignments are represented by the following:

S_p -- The set of partitions.
R_me,{own},p -- The mapping of major elements to the partitions which own them.

A key aspect here is that each major element is assigned to an owning partition, and this owning partition represents the processor that will be responsible for calculating all new field values for that major element. This is essential for computing the direction data must be passed between partitions as well as calculating the size and compute load for each data model partition and communications loads for each communications link between partitions.

The first step in partitioning the data involves getting the element members that are the contents of each partition for each element type. This is done by using the relation compose operations to project the partitioning of the major elements onto each of the other element type sets in the data model.

A. Partition Contents

As shown in Fig. 4 above, each partition must include its owned major elements and the full contents for every element type on which the calculations for these major elements' field values depend. The contents of the partitions also need to be broken out into categories of private; pass (owned and shared ); or receive (being not owned, but needing shared) from other partitions.

The major elements that must be present in each partition may be limited to the above owned major elements. A common case however is, while computing field values for a given major element, access to values from "neighboring" major elements is needed, defining a ghost region of major element data, as in Fig. 5 above, that must be copied to the local partition. To use ghost regions the full collection of major elements present in each partition must include those receive neighbor major elements also. The full collection of major elements that must be represented in each partition may be generated via whichever of the following applies to the given model implementation:

If the calculation of major element field values depend only on the subordinate element types (no ghost regions), then only the own major elements need be in each partition giving

R_me,p = R_me,{own},p
If the calculation of major element field values depends on the major element neighbors which share a secondary element (such as zones sharing faces) then the needed full major elements subset represented in the partitions are augmented by first getting these "neighbors" for every major element via their shared secondary elements by getting the "neighbors" relation

R_{me,{se_neighbors},me} = R_se,me^-1 * R_se,me

then generating the expanded contents of the partitions by projecting the own elements subsets to include their immediate neighbors in the full element subsets.

R_me,p = R_{me,{se_neighbors},me} * R_me,{own},p

If more "levels" of ghost regions are required this last compose can be repeated as many times as needed.
If the calculation of major element field values depends on the major element neighbors which share a tertiary element (such as regions sharing the vertices of their faces) then the needed full major elements subset represented in each partitions are augmented by first getting the "neighbors" for every major element via their (indirectly) shared tertiary elements by first collapsing the indirection

R_te,me = R_te,se * R_te,me

then using that to get their "neighbors" relation

R_{me,{te_neighbors},me} = R_te,me^-1 * R_te,me

then generating the expanded contents of the partitions by projecting the own elements subsets to include their immediate neighbors

R_me,p = R_{me,{te_neighbors},me} * R_me,{own},p

and if more "levels" of ghost regions are required this last compose can be repeated as many times as needed.

Once the major element ownership assignments are made they can be "projected" via relation composition to the other element types, getting the full list of each element type that must be represented in each partition as follows:

R_se,p = R_se,me * R_me,{own},p
and
R_te,p = R_te,se * R_se,p

The full assignment of elements to the partitions in which they must be instantiated, whether as own or receive elements, is know determined. To get the full contents for each partition these relations merely need inverted as

R_p,me = R_me,p^-1
R_p,se = R_se,p^-1
R_p,te = R_te,p^-1

The full contents of each partition is now known for this partitioning. This, in conjunction with the size of each element object instantiation, is later used to estimate the space requirements for each partition.

To understand the computational needs of each partition and to generate communications maps among the partitions it is still necessary to know which elements are "owned" by each partition.

B. Element Ownership by Partitions

Once the relations above describing the associations of each element with one or more partitions have been calculated many of the member elements in the relation R_E,p should reference only one partition. By assigning the ownership of those elements to that one partition any possibility of their associated field values needing passed between partitions is eliminated, greatly reducing the amount of inter-process passing of element data needed.

The three categories of ownership relations needed for each partition, private, pass, and receive, define independent subsets that cover the full set of members of the partition. The last two, pass and receive, define the elements that are in each partition's share subsets, also known as the "shadow regions" illustrated in Fig. 6 above.

The ownership is uncontested for the private set members, and they do not need their attribute field values communicated. These private members can be represented in the subset given by those element set entries with only one partition range set reference. Using the generic E, as this must be done for each element type, a field of boolean private flags (F_private,E) can be derived, then the field values can be used to define the subset of elements that are private for each partition as follows:

F_private,E = (FieldOf(RefCounts(R_E,p)) == 1)

Then the members of S_E that are private in any partition are identified as a separate subset of S_E via

S_{E_private} = Subset(S_E, IndexTrue(F_private,E))

and its subset relation (which enumerates the parent members in the subset) is given by

R_{E_private,E} = SubsetRel(S_{E_private})

The relational mapping of the private elements to the owning partitions is then derived as

R_{E_private,p} = R_{E_private,E} * R_E,p

The actual indices in the global element set S_E of these private members of each partition may be enumerated via the composition which remaps their subset indices to the global indices as

R_{E,{private},p} = R_{E_private,E}^-1 * R_{E_private,p}

The private global set member contents of each partition may be listed as the references of a mapping from the partitions to these members via the inverse

R_{p,{private},E} = R_{E,{private},p}^-1

At this point it is useful to identify the elements that are shared by two or more partitions also, but these are just the members of each partition that are not private, and are given by

R_E,{share},p = R_E,p - R_{E,{private},p}

or, the convenient inverse that maps the parttions to their shared global element set member indices

R_p,{share},E = R_E,{share},p^-1

The ownership of the shared elements is significant in determining which partitions are to calculate the elements' field values. Choosing this ownership also determines to which partitions those values must be passed.

At this point any assignment of the shared members of all but the major elements to any one of the partitions that shares it can be made. Only the abstraction for that ownership of the shared members is needed here. The passing partition relations are identified as

R_E,{pass},p

with

R_p,{pass},E = R_E,{pass},p^-1

Also at this point the full ownership mappings for each of the element types to the partitions can be generated as

R_me,{own},p was given at the beginning of the paper. All the ghost region elements that may be present in a partition are already own for some other partition, and therefore all receive elements in all other partitions that share them.
R_se,{own},p = R_{se,{private},p} + R_se,{pass},p

and
R_te,{own},p = R_{te,{private},p} + R_te,{pass},p

It is useful to be able to subdivide the calculations at this point to generate the sets and relations that should appear for each processor partition independently. This would allow the calculations which follow to be done on separate processors. The following generates the element subsets for each partition. This allows the separate communications maps to be based on them. Using the mappings from above that maps the partitions to the elements they contain R_p,E, the subset of elements contained in each partition are generated via

R_p[i],E = Extract({i}, R_p,E)

with

S_E[i] = Subset(S_E, Range(R_p[i],E))

and

R_E[i],E = SubsetRel(S_E[i])

Similarly the pass subsets may be derived from R_p,{pass},E, giving
- S_{E[i]_pass} and
- R_{E[i]_pass,E}
the receive subsets may be derived from R_{p,{receive},E}, giving
- S_{E[i]_receive} and
- R_{E[i]_receive,E}
and
the share subsets may be derived from the above as
- S_{E[i]_share} = S_{E[i]_pass} + S_{E[i]_receive}
- R_{E[i]_pass,E} = SubsetRel(S_{E[i]_share})

These must map the partition subets to the global element member indices so that they can be matched between partitions, as the S_E[i] member indices are local indices relevant only within its ith partition.

At this point the elements whose field values must be computed in each partition are now known, and the computation load for each partition can be estimated. This is done in the later section, "Computing Loads".

Using the above relations for the various sharing and ownership assignments the communications maps may now be generated.

III. Communications Maps

Once the ownership of each element is known the actual communications needs for each element type's shared data can be derived. The communications maps that must be generated for each partition include which elements are to be sent to and received from each other partition for each element type. This allows the shared elements' field values that are to be shared to be passed from the elements' owning partition to their receiving partitions. The "passing of an element" in this context actually indicates the need for passing those property or attribute field values that change over time for those elements that must be shared, even though many parallel models pass all the field values associated with those pass elements.

Communications maps consist of the following details:

The partitions from which non-empty messsage blocks must be passed and the partitions to which they must be passed, also known as the needed communications links,
A "gather" mapping of which element members in the source partition should be placed into the message block for each element type and each destination partition to be passed over each outbound communications link,
A "scatter" mapping of which element members in the destination partition will be received in the message block for each element type from each source partition to be received over each inbound communications link,

The "gather" mappings must map from the "from" partition element member indices to the indices in the message block, while the "scatter" mappings must map from the message block indices to the "to" partition element member indices.

A. The Inter-Partition Message Blocks

The pass elements' field values must be passed to other partitions after each calculation, and each partition's process must know where to pass it. Then each partition must expect to get its receive elements and know which elements are to come from each other partition. Once these are determined then the elements in each message block being passed between a pair of partitions can be determined.

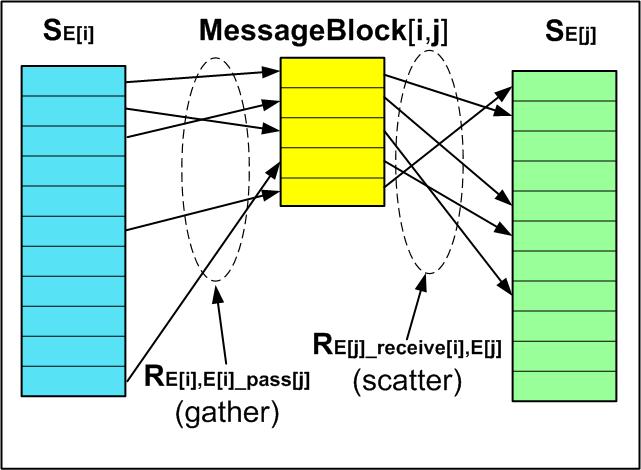
Figure 7: Sharing Message Blocks

Deriving the mapping of elements to be passed from partition i to partition j is a matter of finding the passed element members in S_{E[i]_pass} that are also in S_{E[j]_receive}, by matching their global S_E member indices.

S_{E[i]_pass[j]} = S_{E[i]_pass} ^ S_{E[j]_receive}

which is a subset of S_E whose elements are enumerated in the subset relation given by.

R_{E[i]_pass[j],E} = SubsetRel(S_{E[i]_pass[j]})

which defines the global member indices to be placed into the message block that is to be passed from partition i to partition j and therefore is also the subset (and ordering) to be expected to be received from partition i by partition j with the content ordering defined by the subset relations

R_{E[j]_receive[i],E} == R_{E[i]_pass[j],E}

and the message block set is defined by the subsets, as their size and and parent set member reference orders are the same, with

S_{E[j]_receive[i]} == S_{E[i]_pass[j]}

Once these are found then the subsets of elements in each partition that are to be included in the message block for each receiving partition can be found.

B. The Local Partition Gather/Scatter Maps

The local "gather" mapping is merely the mapping of the pass message block contents to the local element indices in the order the members occur in the message boock as

R_{E[i], E[i]_pass[j]} == R_E[i],E * R_{E[i]_pass[j],E}^-1

and the local "scatter" for extracting the member values into the receiving partition is given by

R_{E[j], E[j]_recieve[i]} == R_E[j],E * R_{E[j]_recieve[i],E}^-1

These allow the ordered mapping of the partition i element members' field values to be gathered into a message block in partition i, the block to be transferred to partition j, then the message block contents scattered into the corresponding fields for the correct element set members in partition j.

C. Partition Communication Links Graph

Each element type's shared members mappings can be used to generate a relation mapping from the partitions through the shared subsets to other partitions that share those elements. Using the generic element designator E the following should be repeated for each element type to get the partition to partition links for them:

R_{p,{E_share},p} = R_E,{share},p^-1 * R_E,{share},p

Figure 8: Communication Links Graph

and by aggregating the links for all of the element types to get the links of the complete graph of partitions that share data with one another by

R_{p,{share links},p} = R_{p,{me_share},p} + R_{p,{se_share},p} + R_{p,{te_share},p}

Since the relation is a mapping from the set of partitions back to the set of partitions its range and domain sets define the nodes (S_p) and the relation R_{p,{share links},p} defines the links of the complete communications graph.

IV. Calculating Loads

Loads on each partition may be estimated for each of three criteria, space requirements, computational time, and communications time.

To estimate loads on the processors, both size and computational,the number and types of elements in each partition must be known. This is given by R_p[i],E for each element type over the ith partition, given by the derived sets S_E[i], for all i in [0, Size(S_p) - 1].

The space loading is generally considered an absolute limiting factor, and is not considered in rebalancing unless the space requirements for one or more partitions exceed the available space threshold for that partition's processor. Of course, when adaptive mesh refinement (AMR) [8] is performed dynamically this can be a concern each time step, as the number of elements may change that often. For the purpose of this paper the static size case is considered, but using the approach in this paper this can be easily extended to be recalculated each time step or as mesh refinements are added or removed.

Computational loads and communications loads are often specified via the time to perform the needed task. These are often directly measured, then the measured time values are used to predict future expected loading. They may also be directly measured, then normalized by the architecture-relative performance details. Architecture performance details are converted from times to performance factors by dividing the measured time of performance by the amount of data processed or communicated during that time. This normalized performance factor may then be used to scale other loads for estimates of the comparative performance of the code processing or communications times on nonhomogeneous environments.

A. Space "Loads"

In most models the amount of space that is taken up by each element type can be considered fixed, so the space loading for each partition can be easily calculated via

       E_count[i] = Size(S_E[i])

and computing the size of each field over that element type

       F_{j, E[i]}= GetField(S_E[i], j)

       field_size[j, i] = E_count[i] * ValueSize(F_{j, E[i]})

giving the total fields size, the dominant contributor to the model size in the partition, for that element type in that partition as

       E_fields_size[i] = ∑_j(field_size[j, i])

Then, by summing over the various element types the total model size for the partition and its numbers of element members can be estimated as

       total_size[i] = me_fields_size[i] + se_fields_size[i] + te_fields_size[i]

Similarly the sizes of any SRF relations, which may also be major size contributors in some cases, may be calcuated, then these size requirements can be added across the element types giving the total size estimate for the given partition for the data model.

Of course, there is also the space needed for buffers for composing message blocks and the fixed overhead of the problem metadata to be considered, but these are often small and fixed, making them less significant than the model element count dependent sizes included above.

B. Computational Loads

The computational load quantity may be estimated for each partition by estimating the computational load for each field that must be calculated. This loading must include accessing the field values that must be used in those calculations, usually through indexing into arrays. The above model manipulations allow easy estimation via any one of the following computational load estimation approaches:

Estimated mean computational requirements for each element type,
Estimated individual element set member computational requirements, and
Directly measured individual element set member computational requirements.

The first just requires multiplying the number of element set members of each type in each partition times the mean computational load for that element type, then summing the products for each partition. The second and third merely require summing the element set member's computational loads for all the element set members of each element type for each partition. These load estimates can be repeated each time step if load balancing is essential to the model being used. These sums for each partition are compared in all three cases to determine the relative loading of the partitions.

Of course, for nonhomogeneous processors the directly measured times in the three "loadings" above must be "scaled" by the comparative speeds of the processors before they can be meaningfully adjusted for moving loads between processors.

C. Communications Loads

Communications over a single homogeneous interconnection, such as a common ethernet, forces all communications loads to compete for the common bandwidth. Such shared bandwidth can cause many processors to sit idle while waiting for their opportunity to communicate their data message blocks. Generally some way is considered for separating the communications into multiple channels to reduce the competition for communications bandwidth to reduce these processor wait times.

Often parallel and distributed processes use separate communications channels shared among isolated processor groups, even just point-to-point communications between processors. Of course, this requires that other channels be available for communicating outside the dedicated communications groups.

Since all communications between processors above is defined as single partition pair message blocks then it defines a simple point-to-point communications pattern. Using an overlay of the point to point partition communications links onto the desired communications interconnect architecture and any "transmission layers" which moderate sharing and routing of messages can allow a wide variety of matchings of the needed point-to-point channels and the capabilities of the communications architecture topology.

One criteria that should be observed to minimize communications needs is to assure that major elements found to be "adjacent" via the dependency links calculated above are kept together in partitions as much as possible. These "adjacent" major elements generally define the locality of needed communications, and by grouping them much of the data sharing is kept inside the partition, rahter than forced to cross between partitions.

For this paper only the simple point to point interprocessor communications loading is derived, but methods for extending to more complex bandwidth sharing configurations are discussed.

The communications links must pass the message blocks described above between processes. The form of communications link can greatly affect the bandwidth that is available, and the maximum bandwidth of each link determines the time in which a given volume of message traffic can be conveyed.

The global inter-partition communications link needs are given by

R_{p,{receive},p} = R_p,{pass},E * R_{p,{receive},E}^-1

defining the links for the graph of partition to partition communications that are needed. This is the point to point topology that must be overlayed onto the hardware architecture's available communications link topology.

The next step is to estimate the quantity of message load that must be conveyed over each of the links above. First, a relation set is defined over the tuples of the above communications graph links relation. This allows the creation of a field of communications load values to be accumulated as the message block sizes are calculated for each link. Second the message block sizes for each communications link are added to the proper entry in the communications links loading field. From above the number of elements for each element type that must contribute their changed field values to the message block are identified for each partition to the ith partition by R_{p,{pass},E[i]_receive} which allows the extraction of the elements for a single element type and partition to partition (k, i) link by

       R_{p[k],{pass},E[i]_receive} = Extract({k}, R_{p,{pass},E[i]_receive})

and the number of elements in the message block to traverse from partition k to partition i is

       E_count[k,i] = Size(S_{E[i]_receive}[k]

Once the elements for a given element type that contribute to a given message block are identified then the message block size can be estimated by adding the field value sizes for those fields that must be passed. Only those fields that may change values each time step need be included, giving, for each such field (indexed by j) over that element type

       F_{j, E[i]} = GetField(S_E[i], j)

The total message block space it requires is given by

       field_size[k, j, i] = E_count[k, i] * ValueSize(F_{j, E[i]})

and the total message block space required for all the fields that must be passed for the given element type is given by

       E_fields_size[k, i] = ∑_j(field_size[k, j, i])

Since the element data for all the element types that must be passed over that link may be more efficiently passed as a single message rather than separate messages per element type the total message block size becomes the sum of the E_fields_size[k, i] values for each of the element types.

This model enables much more complex variations on the communications load estimates because once the loading for each point to point link is calculated they can be combined when message block partition links must share a physical link, getting the total block size loading for each physical link during each time step data transfer.

D. Load Shifting Approaches

Load shifting is essential when space limits are exceeded in any partitions, and is extremely useful when the computational and communications loads differ greatly between partitions.

Initial load shifting may be done to better balance the initial distribution of elements among the partitions and to compensate for processor and communications link performance variations. In many applications this may be the only time load shifting is needed.

Other applications may have computational loads which change over time or may use AMR at run time to refine specific regions of a model over time, increasing or decreasing the number of elements in some partitions, and thus also the computational and communications loads for those processors. Dynamic load shifting is done during the program run to compensate for these run-time load changes. Dynamic load shifting can be done similar to initial load shifting, but it is useful to estimate actual loading each step and only adjust the element allocations when the load differences exceed some reasonable problem-dependent threshold.

It is obvious that the major elements which need to be shifted should come from among those that are in the share category or, if there are none in that category, then major elements that depend on shared elements of other types, indicating they are near the boundaries between partitions. Moving these major elements between partitions will require moving other secondary and tertiary elements between the partitions also, requiring the accompanying adjustments to the impacted subset memberships, mapping relations, and loading parameters derived above.

If the partition that is overloaded is not a "neighbor" (in the communications topology graph defined by R_{p,{receive},p} above) of the underloaded partition to which load must be shifted then it is useful to generate a "path" of successive element shifts to handle data migrations gracefully. Such multiple-partition load shift repartitioning is handled easily via the above methods.

V. Related Topics

Two major concerns have been voiced over this approach to parallel partitioning:

How can this approach be applied to models not in the SRF representation?
How does the SRF approach scale for exascale problems?

Most generalized mesh, particle, molecular, and network models are easily converted to the SRF representations needed. Models which require a "complete" communications graph will be inefficient, while models that use geometric space "nearness" are easily adapted. Special attention is being give to the automated conversion from the model form of most concern, the rectangular mesh structured model. As time and resources permit other automatic parallelization applications are also being explored.

To handle exascale model partitioning the model element set sizes and the relations that must be manipulated can become quite large. To handle the extremely large partitioning problem the SRF algorithm implementations parallelization is being designed and implemented.

A. Structured Mesh Models into SRF Data Models

Many simulations use rectangular mesh models for their simplicity and ease of understanding. However, the rectangular structure itself uses implicit data element relationships to maintain that "intuitive feel". Adjacency of elements is implicit in that the code merely increments or decrements an index for the neighbor's indices, and if the index goes beyond 0 or some maximum value the indexed element is on a boundary. Both the adjacency and the boundary-ness are implicitly "disguised" in the mesh structure, but define the relationships of "adjacency" and the dependencies of calculations on these adjacent elements' values.. Similarly the associations of major elements to minor elements is often based on some basic index manipulation, because the arrays they are stored in are not of the same dimensionality. Often there must be separate arrays of faces or edges, one for each orientation. These implicit relationships are well understood and easily map into the explicit realtions needed for the SRF representation.

All of these implicit relationships constrain the partitioning of the models onto parallel architectures except in specific index-range based subsets of elements. Due to the complexities caused by the form of the impicit relationships it is even more difficult to use irregular numbers of partitions, shift arbitrary elements from one partition to another for load balancing, or easily generate communications maps for such model variations. Once the problem is expressed in the expicit form of the SRF algebra these variations on partitioning are no longer obstacles requiring ad-hoc workarounds.

B. SRF for Partitioning Exascale Data Models

Exascale parallel partitioning of extremely large models require that the partitioning problem itself becomes extremely large. The SRF algorithms are currently being parallelized for handling excessively large problem data. An exploratory effort is considering "bootstrapping" an implementation of SRF that is described in SRF iteself.

Also, exascale parallel programs require far more complex communications patterns than terascale problems could use. The complexities of aligning communications maps onto hierarchical communications topologies are relatively easy using the SRF data models and basic graph overlay techniques.

VI. Summary

The SRF Algebra is a sets-based abstraction and notation for representing the logical structures of data. By expressing data as sets of object abstractions, property fields over the set members, and relationships between the members of the sets using an algebraic notation gives the designer and analyst a common and logical symbology for tackling otherwise seemingly intractable manual tasks. SRF has simplified the descriptive representations of complex mesh models and the operations needed to perform parallel decomposition and generate the communications maps for the partitioned models. SRF has also been used to represent levels of abstractions for multi-network critical infrastructure models and social networking models. The SRF Algebra is a powerful tool for complex systems modeling and analysis.

The SRF Algebra defines a portable metadata structure in which many diverse model forms may be easily represented, and all the relevant data associations may be expressed in the explicit relations. The sets are simple abstractions for explicitely handling the objects, the fields are just metadata wrappers around the arrays of element property values that already must exist in the models, and many of the relations are just wrappers around association tuples that many models must already store. Only the implit relationships require generating new collections of tuples to make them explicit in the model.

The SRF Algebra abstractions provide the metadata to make explicit most of the relevant implicit associations found in various data models. Levels of abstraction are used to emphasize those relationships that are essential to partitioning the data model and generate the code necessary to scale the code up for substantially larger applications.

References:

James R. Holten III, "SRF Algebra: Foundations", SRFAlgebra_20101116.html 20010-11-11
James R. Holten III, "Sets, Relations, and Fields (SRF) Overview", SRF.html 2007-3-07.
Paul R. Halmos, "Naive Set Theory", Springer, 1974.
Patrick Suppes, "Axiomatic Set Theory", Dover, 1972.
C. J. Date "An Introduction to Database Systems" , Addison Wesley (8th Edition) 2003.
Butler, "SAF Reference Manual", Lawrence Livermore National Laboratory, Jan. 29, 2001.
Larry A. Schoof, Victor R. Yarberry, "Exodus II: A Finite Element Data Model", Sandia National Laboratories, November 1995.
Robert P. Weaver, Michael L Gittings, Galen R. Gisler, Robert F. Coker, Kimberly C New, and Robert M. Hueckstaedt "An Overview of the Los Alamos Crestone Project: Uses for Astrophysical Problems", Los Alamos National Laboratory, AMOS Technical Conference, September, 2004.
Nicos Christofides "Graph Theory: and Algorithmic Approach" , Academic Press, 1975.
Ravindra K. Ahuja, Thomas L.Magnanti, James B. Orlin "Network Flows" , Prentice Hall, 1993.
James R. Holten III, "Parallel MxN Repartitioning", MXNrepartitioning.html 2003-03-18.
Bruce Hendrickson and Steve Plimpton "Tinkertoy Parallel Programming: Complicated Applications from Simple Tools", Proceedings of 10th SIM Conference on Parallel Processing for Scientific Computing, 2001.